Modeling in IceSL with the Lua editor
Author: Salim Perchy (yamil-salim.perchy at inria dot fr)
Welcome to the 2nd tutorial of IceSL. This tutorial is aimed at introducing the basics of modeling shapes in IceSL using Lua. Some familiarity with Lua is recommended before going through this tutorial. Estimated time of completion is 15 minutes.
- We’re going to model a six-sided die1 using CSG (Constructive Solid Geometry) with the Lua editor of IceSL. Start IceSL and create a new file (File → New), answer no when prompted to save. Throughout this tutorial we will be writing code on the Lua editor (left area of the main window).
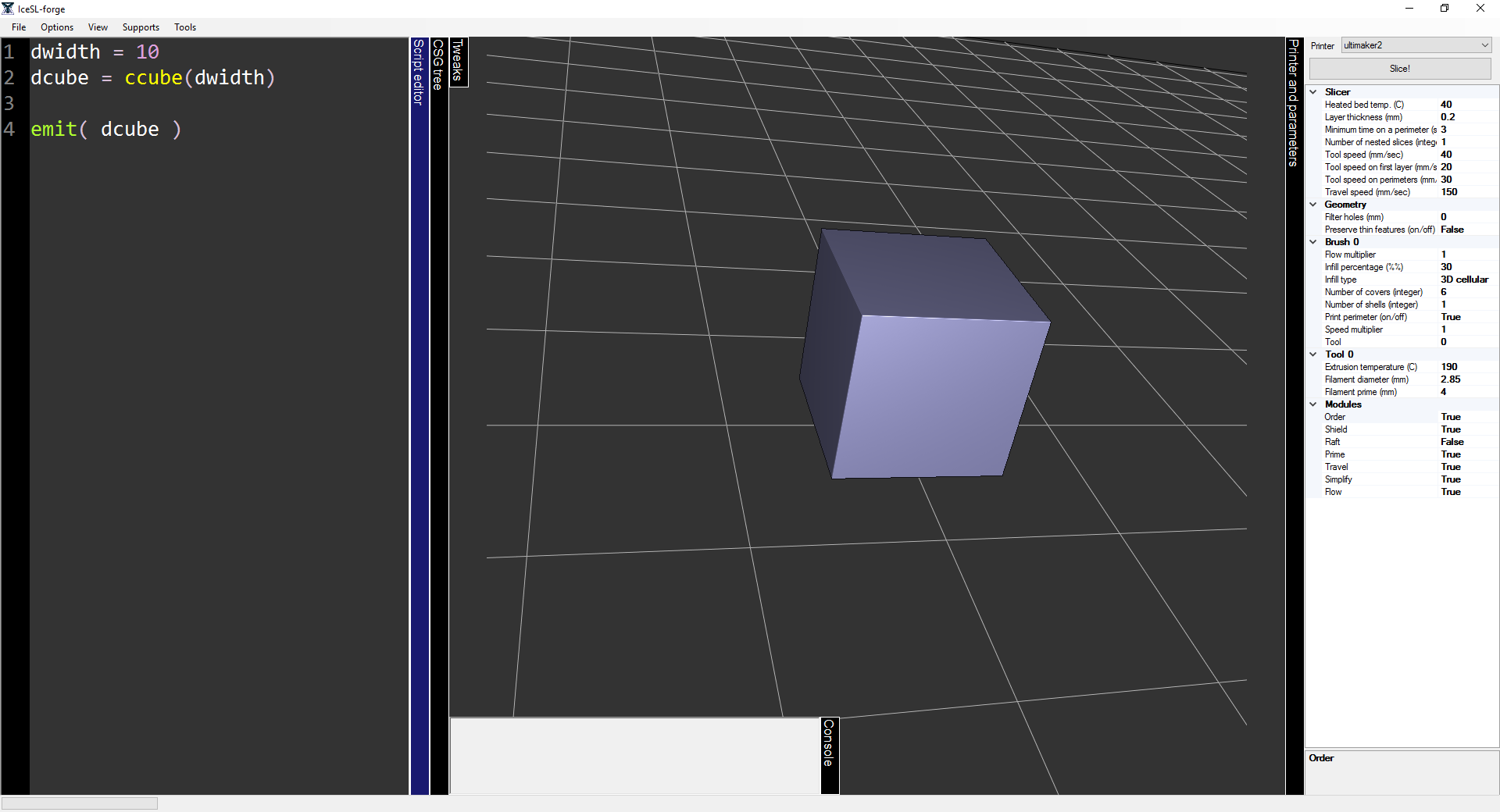
- We first, create the base cube that makes up the die. For this, we parametrize the size with variable dwidth and create a centered (on the origin) cube with the following code:
dwidth = 10
dcube = ccube( dwidth )- The ccube directive creates a centered cube of width dwidth and we assign it to variable dcube. To visualize the created volume we need to emit it:
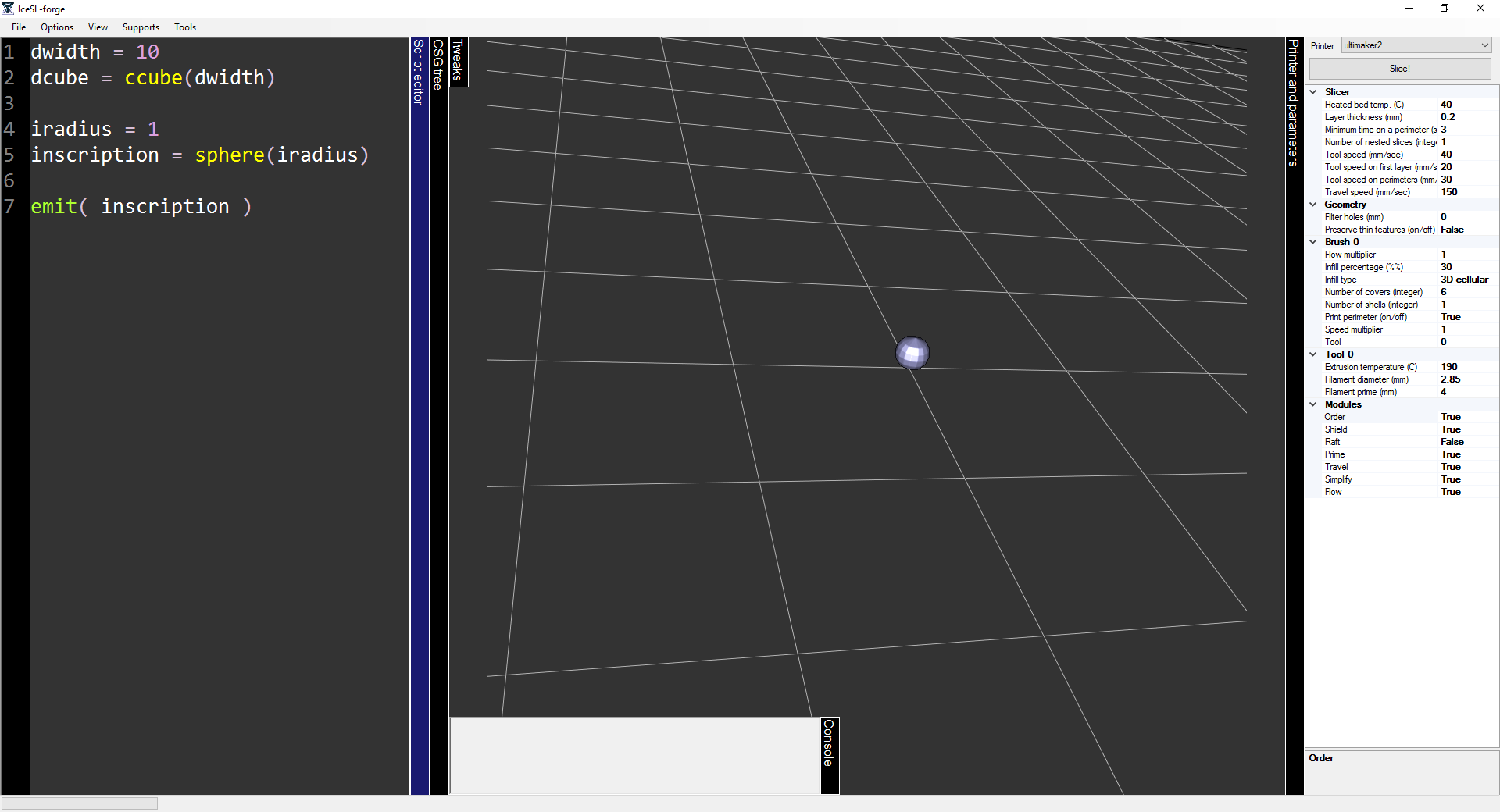
emit( dcube )- For the circular inscriptions identifying each side of the die to its corresponding number we will create a sphere of radius 1. Before proceeding, discard the line that emits dcube. The sphere is created as follows:
iradius = 1
inscription = sphere( iradius )- Just as we did with dcube, we can emit the sphere through the variable inscription to visually check the shape we’re modeling. Again, discard the line that emits the sphere before continuing onto the next step of the tutorial.
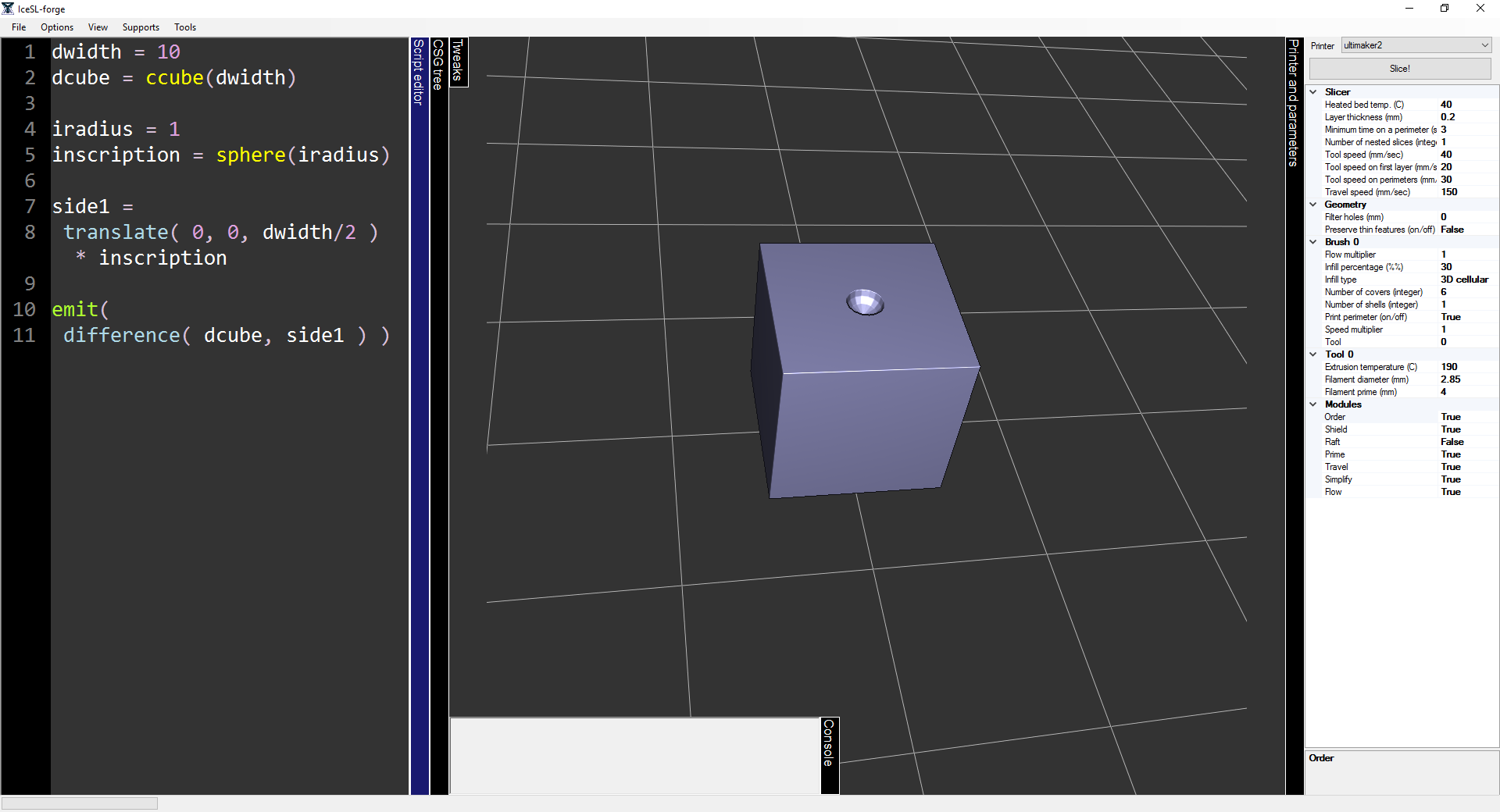
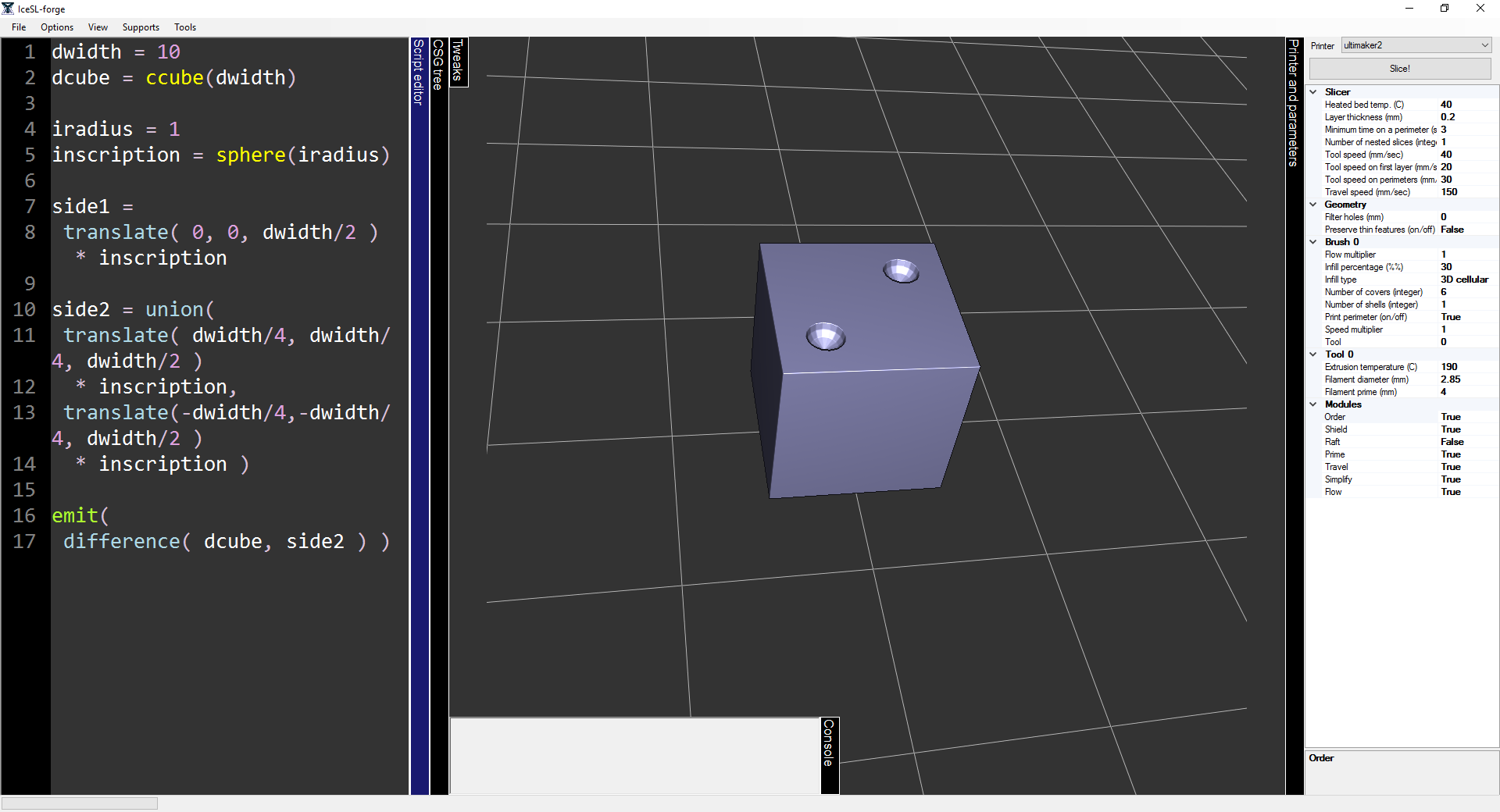
- We begin by sculpting the upper side of the cube with the inscription corresponding to the value 1. To achieve this, we center the sphere, translate it to the upper side of the cube and save it in variable side1. We emit both figures to have visual feedback:
side1 = translate( 0, 0, dwidth/2 ) * inscription
emit( dcube )
emit( side1 )- Obviously, the inscription is supposed to be carved and not added onto the dice. In order to do this, we use the boolean operation called difference that subtracts the volume of one shape from another. In this case we subtract the volume of the inscription (sphere) from the volume of the dice (cube). Remove both emits and replace them by:
emit( difference( dcube, side1 ) )- We still carve the top of the cube, but this time we do the inscription for the value 2. To do this we need two spheres. There is no need to create an extra sphere, we can use the boolean operation called union. This operations adds the volume of one shape to another, this way we can construct the correct inscription onto the variable side2:
side2 = union(
translate( dwidth/4, dwidth/4, dwidth/2 )
* inscription,
translate(-dwidth/4,-dwidth/4, dwidth/2 )
* inscription )- Pay close attention how we translated each inscription to the upper right corner and lower left corner on the upper side of the die. As usual, we could have some visual feedback by emitting the difference between the dcube and side2 variables.
- We continue creating the other inscriptions for the other values (i.e., 3,4,5 and 6). When boolean operations take more than two arguments, we pack the arguments between braces. Notice how the inscription of the side with value 6 is translated to the lower side of the die and not the upper. Try to code one of these sides by yourself!
side3 = union{
translate( 0, 0, dwidth/2 )
* inscription,
translate( dwidth/4, dwidth/4, dwidth/2 )
* inscription,
translate(-dwidth/4,-dwidth/4, dwidth/2 )
* inscription }
side4 = union{
translate( dwidth/4, dwidth/4, dwidth/2 )
* inscription,
translate( dwidth/4,-dwidth/4, dwidth/2 )
* inscription,
translate(-dwidth/4,-dwidth/4, dwidth/2 )
* inscription,
translate(-dwidth/4, dwidth/4, dwidth/2 )
* inscription }
side5 = union{
translate( 0, 0, dwidth/2 )
* inscription,
translate( dwidth/4, dwidth/4, dwidth/2 )
* inscription,
translate( dwidth/4,-dwidth/4, dwidth/2 )
* inscription,
translate(-dwidth/4,-dwidth/4, dwidth/2 )
* inscription,
translate(-dwidth/4, dwidth/4, dwidth/2 )
* inscription }
side6 = union{
translate( dwidth/4, 0,-dwidth/2 )
* inscription,
translate(-dwidth/4, 0,-dwidth/2 )
* inscription,
translate( dwidth/4, dwidth/4,-dwidth/2 )
* inscription,
translate( dwidth/4,-dwidth/4,-dwidth/2 )
* inscription,
translate(-dwidth/4,-dwidth/4,-dwidth/2 )
* inscription,
translate(-dwidth/4, dwidth/4,-dwidth/2 )
* inscription }- To correctly place each inscription on a different face of the die cube we need to abide by one invariant: two opposing sides must always add 7. For example we can place the inscription of value 1 on the upper face and the inscription of value 6 on the lower face, as such they face each other and their sum is 7. For the other sides, we must rotate them accordingly so they also add 7:
sides = union{ side1,
rotate( 90.0, Y) * side2,
rotate(-90.0, X) * side3,
rotate( 90.0, X) * side4,
rotate(-90.0, Y) * side5,
side6 }- Now we are ready to construct the whole geometry of the die. By having the variables dcube and sides containing the cube die and its inscriptions respectively, it is then fairly simple to join them:
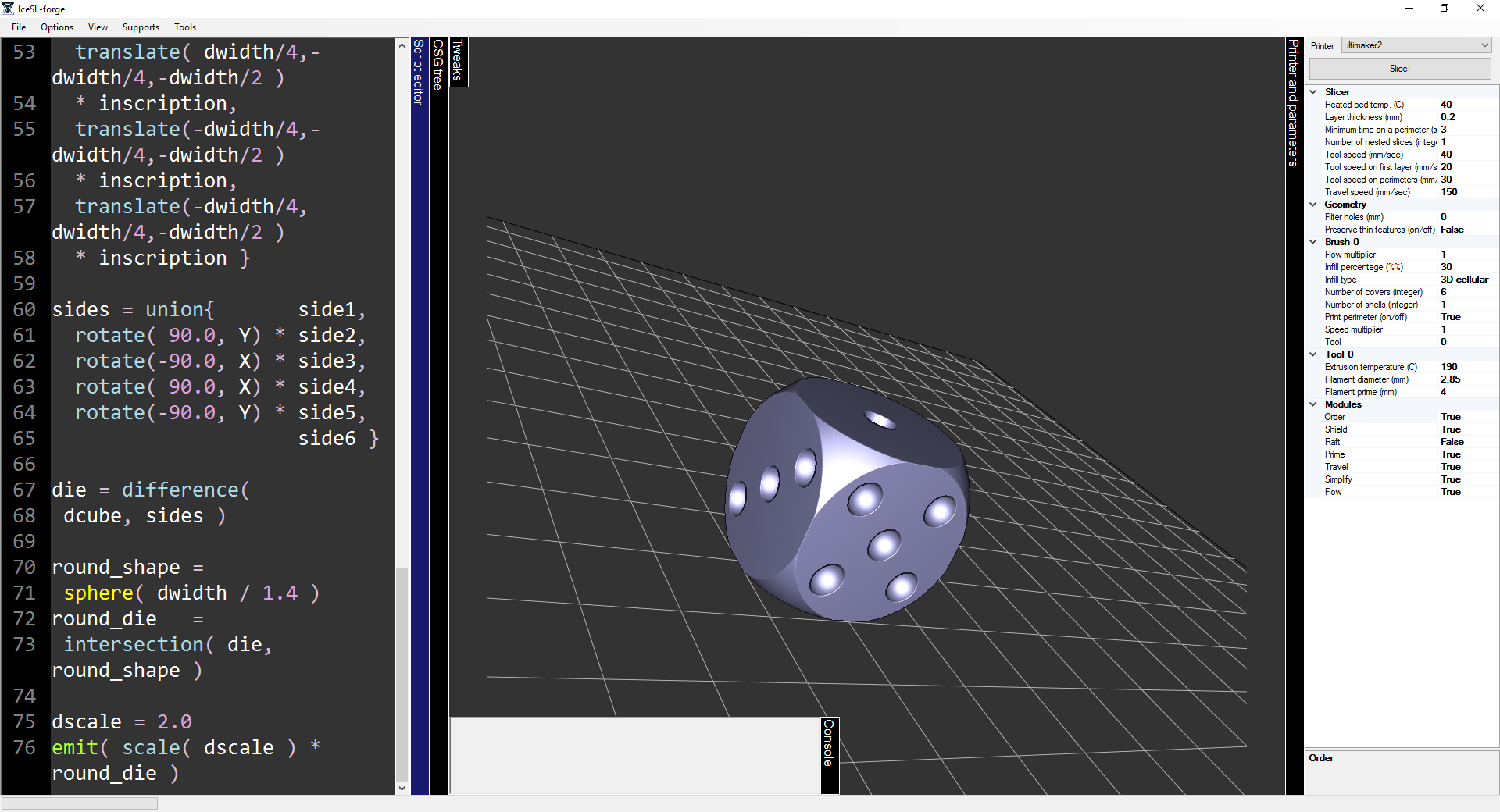
die = difference( dcube, sides )
emit( die )- Finally, notice how the final shape of the die has pointy corners. This may be undesirable due to the damage that might be caused by throwing the die. We can elegantly solve this by using boolean operations again:
round_shape = sphere(dwidth / 1.4)
round_die = intersection( die, round_shape )
dscale = 2.0
emit( round_die * scale( dscale ) )- We create a sphere of roughly half more the size of the die cube and apply the boolean operation intersection. This operation calculates the volume common to the two volumes and in this case it’s what gives the round shape to the die. For convenience, we add a scale factor dscale that is applied to the final volume. This scaling serves as a global scaling factor for the final volume without tweaking the initial values of the components (e.g., die width, inscription radius, etc). The full source code to the Lua script can be downloaded here.
Exercise!
Using the Lua editor of IceSL, try to model the figure of a 4-sided die. Some tips on how to do this:
- IceSL comes with a variety of commands to construct volumes, here you can find a complete reference. Using spheres and the convex_hull function provides a simple way to create the body of the dice (thanks to user Maze Mietner for suggesting this approach!).
- Etching numbers on each side of the die can prove difficult using only primitive shapes (e.g., cube, sphere, etc.). See the scripting documentation on how to produce text geometry.
1. Six-sided colored dice image made by user Diacritica from Wikimedia Commons licensed under CC BY-SA 3.0